Skimpression - Love and Math: The Heart of Hidden Reality

The second book I read is called Love and Math: The Heart of Hidden Reality, by Edward Frenkel. It was kind of hard to just skim this book but I did read a good chunk of it. I was really looking forward to reading this book as the review given by the students reading it previously gave it an outstanding evaluation. To be honest it was hard for me to get involved with the book. Frenkel has an interesting story of how he got in to mathematics and his struggle to pursue more education with his Jewish heritage, but he incorporates these math problems or his work on math problems amidst his personal story and that for me made it hard to follow. Perhaps, if he made two books with one being his work with mathematics and the other being his personal story, then that would be better.

Math Inspired Fashion

In this capstone class we have gone through years and years of mathematics and the notable mathematicians included. We looked at foundational theorem's as well as some of the unusual innovations. For this last blog post I am digging deeper into the applications of math, more specifically, the influence it has on fashion design. I credit Professor Golden for sparking my interest in this relation as he provided some information on William Thurston's influence on the designer Dai Fujiwara. This might seem a bit out of left field but, believe it or not, I do have a passion for fashion and with my mathematical intrigue I found it fascinating the some of the connections I found.
1. Eri Matsui: This Japanese fashion designer caught some eyes when she presented a collection of designs inspired by klein bottles, Escher patterns, the Fibonacci sequence, and knot theory. Matsui searched for ways to make women look beautiful which initially led her to the Golden Ratio. She uses Mathematica, an application for computations, in the design process to "compare between things generated from a computer and things created with human passions."

 2. threeASFOUR: This avant garde design team creates designs based on a complex mathematical function. These swirls, circular forms, and fractal like prints come from something known as a Julia set. A Julia set, as defined by oxford dictionaries, is a set of complex numbers that do not converge to any limit when a given mapping is repeatedly applied to them. In some cases the result is a connected fractal set. Here are some of the pieces threeASFOUR has created: 

What this design label has created is absolutely amazing to me and very inspiring. My future isn't yet defined by a certain job and this just shows me more ways that mathematics can be applied.

3. Amila Hrustic: Hrustic took inspiration from the five platonic solids (the tetrahedron, cube, octahedron, dodecahedron, icosahedron) to create "Plato's Collection." As these solids are suggested to be the building blocks of the universe, Amila used these shapes as a basis for her designs. She crafted these black and white dresses using recyclable paper and textiles and forming them almost all by hand without any “machines or things that could damage body or nature,”as Hrustic describes.

Fashion is an open ended industry and to involve a mathematical perspective adds to this infinity. This research, though I am sure I just cracked the surface, has enlightened me and has motivated me to look in to this a bit more. Perhaps graduate school in textile design is in my future, who knows? 


References:
1. - http://www.wolfram.com/mathematica/customer-stories/japanese-fashion-designer-eri-matsui-puts-mathematica-on-the-tokyo-catwalks.html

2. - http://cmediamktg.com/fashion-design-inspiration-complex-mathematics/
- http://www.style.com/fashionshows/review/S2007RTW-TAF/
- http://www.oxforddictionaries.com/us/definition/american_english/Julia-set
- (photo) - http://www.stylebistro.com/runway/Threeasfour/New+York+Fashion+Week+Fall+2012/Details/X2fhGtQX88O
- (photo) - http://metamorphosis-style.tumblr.com/post/20607962779/threeasfour-fall-2012

3. - http://www.ecouterre.com/sarajevo-artist-creates-math-inspired-origami-dresses-from-paper-textiles/
- (photos) - http://www.dezeen.com/2010/11/23/platos-collection-by-amila-hrustic/

Women in Mathematics

There is no question that male mathematician's like Euler, Newton, and Euclid made remarkable impacts in the world of math, but there are many women of the past that did the same. When I think back to middle school and high school I don't remember learning about relevant women in the field of math, or in science for that matter. Here are a few women that made contributions to mathematics:

1. Amalie Noether: Noether was born in Germany into an already very mathematical family. She was highly influential in the world of mathematics. Amalie published papers that dealt with abstract algebra and ring theory. It was debated whether math should be more applied rather than conceptual, but Noether's work on abstract algebra led to principles unifying algebra, geometry, linear algebra, topology, and logic. Her most notable impact to mathematics is with her theorem, known simply as "Noether's Theorem." This boils down to differentiable symmetry of the action of a physical system, with respect to a Lagrangian function, has a corresponding conservation law.

2. Maria Agnesi: Agnesi, born in Milan in 1718, is most recognized for her work on differential and integral calculus as shown in her book, Analytical Institutions. It is said that she originally wrote Analytical Institutions for her brothers but it was eventually published in 1748 for the greater good. The first few sections of this textbook include the analysis of finite quantities, maxima, minima, tangents, and inflection points. Also included in this text is Agnesi's equation to the cubic curve, shown below, now known as the "Witch of Agnesi," which is y = a*sqrt(a*x-x*x)/x.

3. Sophie Germain: Germain is one of the first mathematicians, male or female, to come up with part of a solution to Fermat's Last Theorem in regards to a large class of exponents. A Sophie Germain prime is a prime number n where 2n+1 is also prime. Her prime numbers make appearances in number theory and even cryptology.

4. Florence Nightingale: Florence Nightingale focused more on statistical findings, as she would collect, tabulate, interpret, and present graphical displays of descriptive statistics. The well known and widely popular pie chart was preceded by Nightingale's "polar-area diagram," which shown below.

These women had some trouble being able to get their ideas out in to the public as skepticism ran high when seeing a female's name in a heading. Some of the women went as far as publishing their work under a male name to get recognition.

Equality between men and women can be a touchy subject so I will tread lightly, but it has come a long way. Generally, we tend to associate men to fields of study in the math and sciences which according to a study done by the National Science Foundation (http://www.nsf.gov/statistics/wmpd/2013/pdf/tab2-9_updated_2014_05.pdf) we aren't far off as there are almost 4 times the amount of males that enter the field of engineering than females. To further this though, some may believe that males are better suited for these fields of study rather than women. This stereotype or theory that people may have might be impacting the number of women entering math and science related fields. It is interesting to follow the history of women in mathematics and see how far our society has come because of them.

On a personal level, I came in to college declaring a major in engineering and my Engineering 101 class would provide some great evidence of the lopsided ratio of men to women in a science related field. There was only one other female in my discussion class of EGR 101 out of roughly 40 students! I spent about 1 1/2 years taking classes for this major and I will say that I did feel that many of the guys felt as if they were superior to the women in terms of there technical skills and ability to grasp the concepts. As I transitioned to a mathematics major I noticed many more females in my classes and that feeling of male dominance was non existent. I felt the field of Engineering was just not for me and perhaps I switched majors because of the constant pressure I felt to prove myself to the guys, but if this were the case it was a subconscious thought. Whatever the case may be, I am very happy I switched to mathematics!

References:
http://www.agnesscott.edu/lriddle/women/agnesi.htm

http://apcentral.collegeboard.com/apc/members/features/9371.html

http://www.nytimes.com/2012/03/27/science/emmy-noether-the-most-significant-mathematician-youve-never-heard-of.html?pagewanted=all&_r=1&

https://www.sdsc.edu/ScienceWomen/noether.html

http://en.wikipedia.org/wiki/Noether%27s_theorem

http://www.nsf.gov/statistics/wmpd/2013/sex.cfm

Book Review: The Math Book by Clifford A. Pickover

The Math Book, by Clifford A. Pickover, is a chronological compilation of 250 of the greatest milestones in the history of mathematics involving the greatest mathematicians. To get a glimpse at the vast time frame Pickover covers he starts at c. 150 million B.C. which is when the discovery that ants can "count" their steps came about and concludes with Max Tegmark's Mathematical Universe Hypothesis of 2007. Each mathematical turning point that is described in this book is portrayed in just a one page entry with a corresponding visual that might help with the understanding of the mathematical achievement. Not only were there several theorems and innovations depicted, numerous mathematicians, logicians, philosophers, and scientists were featured. In some instances I would read two or three entries in a row with the same person mentioned, which I found to be amazing.

All of the entries were intriguing, and of course milestones like the Fundamental Theorem of Algebra, the Pythagorean Theorem, and works from Archimedes and Aristotle we included, but I compiled, though hard to pick so few, some of my personal favorites to share:

• Ant Odometer (c. 150 million B.C., pg 18): The Cataglyphis forits, a Saharan desert ant, is able to travel tremendous distances and return to original starting point with a direct path. Light from the sky isn't  the only thing that helps their orientation for travel but this ant seems to have an internal "pedometer" that counts their steps for measuring distances. A few German and Swiss scientists allowed these ants to reach their destination and then would either amputate their legs or add stilts to their legs. The researchers noticed that when the legs were shortened the ants didn't quite reach their starting point and when the legs were lengthened the ants went too far past their starting point.

• Quipu (c. 3000 B.C, page 28): A quipu was a device used by ancient Incas for storing numbers in the form of strings and knots. The Incas lack of writing left them to record everything by a logical-numbering system on these quipus. Speculation suggests that these information systems contained construction plans, dance patterns, and records of human and material resources. One application of the quipu that I found most interesting and a bit gruesome was that it was used as a death calculator.  The chords represented roads and the knots referred to the sacrificed victims. The quipu dismisses the idea that mathematics prospers after writing is developed. Here is an example of a quipu:
  
  

• Rope Around the Earth Puzzle (1702, pg 162): This particular puzzle intrigued me because of its seemingly external complexity but rather simple solution. The question posed is: If you have a rope that wraps around the equator of a sphere the size of Earth, how much longer would you have to make the rope so that it is one foot off the ground all away around the equator? It seems this problem would be much more difficult than the what the answer is, which is 2*pi.  

• Gödel's Theorem (1931, pg 362): Kurt Gödel was a brilliant logician that had quite a few people in disbelief or conflict. His theorem pretty much dwindles down to that mathematics is "incomplete." I included this as one of my favorites because when I was left speechless, or I guess my mind was speechless!

• Mathematical Universe Hypothesis (2007, pg 516): Max Tegmark came up with the hypothesis that "our physical reality is a mathematical structure and that our universe is not just described by mathematics - it is mathematics." Tegmark believes that we discover mathematical structures rather than invent them. One of greatest debates about mathematics is whether it is invented or discovered and Tegmark sheds some light on this. 

Though The Math Book is a relatively quick read, there is a lot of information to take away from it. If mathematics is even in the slight bit of interest to you, I would recommend this book. Some parts of math can be pretty dense and hard to grasp, but Pickover does an excellent job of condensing the crucial information of each milestone in to a one page entry in a manner that is more easily understood. As a bonus the visuals are just as appealing as the milestones! 



Photo from: http://www.nationalgeographic.com/inca/inca_culture_3.html
 

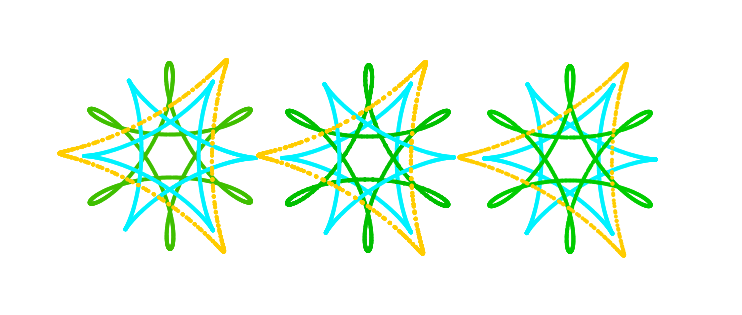
Doing Math: Hypocycloids

A hypocycloid is generated by the tracing a fixed point on a circle in which that circle rolls along the inside edge of the larger circle. I took some time to create a few of my own hypocycloid's using a GeoGebra software. My artistic side kind of got the better of me when doing this exercise as the numerous shapes and designs that could be created were intriguing.

Cardano, a man of many interests of the 16th century, studied hypocycloid's which later became known as Cardano circles. The construction of high speed printing presses were based off of these circular patterns. It would be interesting to see how hypocycloid's and even cycloid's are incorporated in to everyday life. I am sure the engineering world has a lot of use for these designs, but would rather see them as a mechanical curve instead of just a geometrical circle.

Link to Geogebra tool i used: http://www.geogebratube.org/material/show/id/29389

References:

http://math27.page.tl/Gerolamo-Cardano.htm

http://library.iated.org/view/FLOREZ2011DES

Communicating Math: Amicable Numbers

Amicable numbers are two numbers whose factors, not including the number itself, add up to the same value. For instance, since the time of Pythagoras, 220 and 284 is a common example of a pair of numbers that are amicable. If we add up the factors of 220 and remember not to include 220 we get

1+2+4+5+10+11+20+22+44+55+110 = 284.

Similarly, if we add up the factors, expect itself, of 284 we yield

1+2+4+71+142 = 220.

To find other pairs of amicable numbers, Thabit ibn Qurra came up with some general formulas to do so. If

T(n)=3*(2^n) - 1 (also known as the 321 number),

T(n - 1)=3*(2^(n - 1)) - 1,

and

9*(2^(2n - 1)) - 1

are prime numbers, then the numbers

(2^n)*T(n)*T(n - 1)

and

(2^n)*(9*(2^(2n - 1)) - 1)

are amicable. 

As of today, the only values of n that give us amicable numbers following Thabit's stipulations are 2, 4, and 7. On the other hand, these formula's don't work for the thousands of amicable pairs that have been found in recent years. One example is the pair of 1184 and 1210. We are not able to get these two numbers from an integer value n by following Thabit's rules, yet they are still amicable. 

It is interesting to think about why someone would first think to add up factors of a number and try to match the sum of factors for another number. Hundreds of thousands of pairs have been found but will there ever be a sure fire formula that provides two amicable numbers? Are there infinitely many pairs of amicable numbers out there? This concept of amicable numbers is kind of an ongoing mystery that keeps mathematicians curious and searching for more answers. 

Reference:
http://mathlair.allfunandgames.ca/amicable.php

Doing Math: Geometric Tessellation

For this week's post I decided to create a geometric tessellation. You might think drawing repeating patterns would be pretty easy, but as each pattern is added the lines start to cause confusion and mistakes are most likely to be made. My eraser was a much needed tool in completing this tessellation. The one shown below took me about and hour and 45 minutes to make and with the help of just a solo cup and a ruler I must say I am proud of it, though it is not very precise.
Step 1:

With not having a protractor or compass I had to use a cup as a starting point. I traced a circle around the base of the cup and then inscribed a hexagon in to that circle using a ruler to try to make the sides as equal in length as possible. I went off of this hexagon for the rest of them and just a ruler to align the overlapping hexagons. I chose to start with a hexagon of this size as it leaves a fair amount of open space to add more details without loosing the contour of each shape added.

Step 2:

Next I added a smaller hexagon at 3 vertices of the each of the larger hexagons. Then I added irregular hexagons inside some of the larger hexagons as shown above, making sure to repeat this pattern. I knew I wanted to center some polygon around some of the vertices of the large hexagons and adding the smaller hexagons was just the thing to do. Once I did this I thought I would continue with the hexagon theme and fill in the space of the larger hexagons. I held back a little bit to get the "every other" pattern going.

Step 3:

For the finishing touch I outlined every line in sharpie for a more pronounced look and to clearly see the repeating pattern.

Tessellations can be just beautiful pieces of art but they also appear in nature and other everyday items. For instance, honeycombs, floor tilings, glass ceiling framework, and brickwork all incorporate patterns that define a tessellation. Since these are such intriguing designs it is not surprising that marketing and advertising companies use them on packaging and products to grab a consumer's attention. It might be a small pattern but I believe that you will always be able find a tessellation in your everyday life.